Pythagorean Theorem & Converse

Parts of a Right Triangle (Based on Sides)

  • The legs of a right triangle are ALWAYS perpendicular (meet at 90° right angles).
  • The hypotenuse is always across from (diagonal) from the 90° right angle.
  • The hypotenuse is ALWAYS the longest side of a right triangle.

Pythagorean Theorem

Pythagorean Theorem – the sum of the squares of the two legs of a right triangle is equal to the square of the hypotenuse.

  • Hypotenuse is ALWAYS “c“
  • Legs are ALWAYS “a” and “b“
    • “a” and “b” are the shortest sides.
    • “a” and “b” are always perpendicular.
    • “a” and “b” are interchangeable, because “a2 + b2” is the same as (equal to) “b2 + a2” (commutative property of addition).

Converse of the Pythagorean Theorem

Converse of the Pythagorean Theorem – If the sum of the squares of the two sides of a triangle is equal to the square of the longest side, then the triangle is a right triangle.

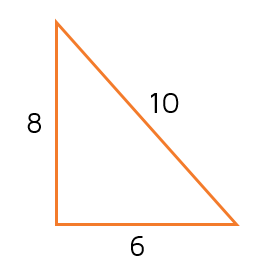
  • See Example (Below) & Ask Yourself:
    1. Is this a right triangle?”
      • Use the Converse Pythagorean Theorem to find out!
    2. What is the sum of the squares of the two smaller sides (the legs)?
      • 62 + 82 Square each Leg
      • 36 + 64 Add the Squares
      • 100 Simplify
    3. Does the square of the largest side (the hypotenuse) also equal 100?
      • Yes, 102 = 100; so, this IS a right triangle!