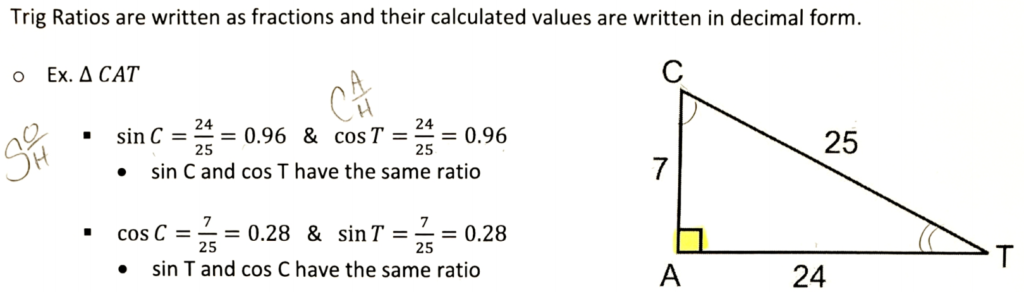Intro to Trigonometric Ratios

Why do we need Trigonometry?

Trigonometry, the branch of mathematics that describes the relationship between the angles and side lengths of triangles. Early explorers used “trig” to plot the stars and navigate the seas.

Today, trig is used in architecture, criminology, interior design, music production, electrical engineering, navigation (travel), and so much more.

What can you use trig for right now?! Watch this video!

Credit: Mrs. B

Notes

  • Trigonometric ratios are tools that can be used to find missing sides and angles of right triangles.
    • In our world, we have angles and distances all around us!
      • The angle of your eyes to the top of a building.
      • The height of your bedroom wall.
      • The distance to your mailbox from your front door.
      • The angle a plane takes off from the runway.
    • You have studied many tools that can be used to find missing sides and angles. The Pythagorean Theorem and the Triangle Angle Sum Theorem are two of these many tools. In this lesson, you will learn another: trigonometric ratios.

Key Terms

  • Trigonometric Ratios: ratios that relate the lengths of the sides of right triangles to their interior angles.
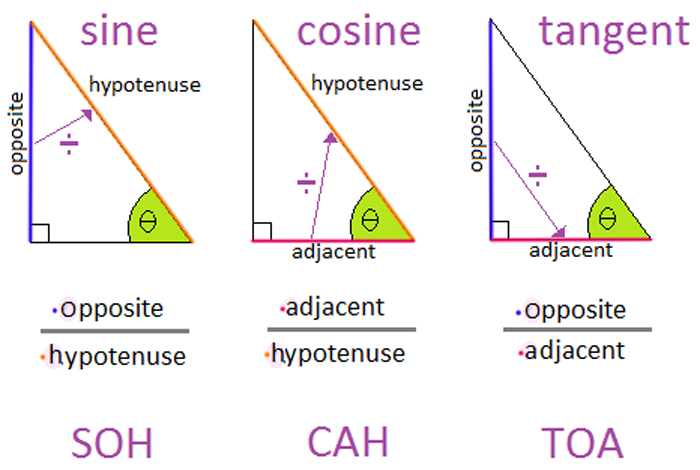
  • Sine: the sine (sin) of an angle is equal to the length of the opposite (opp) side divided by the length of the hypotenuse (Hypot).
    • sin θ = Opp / Hypot
  • Cosine: the cosine (cos) of an angle is equal to the length of the adjacent (adj) side divided by the length of the hypotenuse (Hypot).
    • cos θ = Adj / Hypot
  • Tangent: the tangent (tan) of an angle is equal to the length of the opposite (opp) side divided by the length of the adjacent (adj) side.
    • Tan θ = Opp / Adj

Choosing the Best Tool

Ask yourself, “What tool(s) can I use?” and “How do I know?”

  1. Identify the parts (angles and sides) you are given, or can determine.
  2. Do you have a right triangle?
    • No? You can find missing angles using the Triangle Angle Sum Theorem or other angle theorems. You may not be able to find missing sides “yet” as you need to learn more geometric tools.
    • Yes? See below…
  3. What part (angle or side) are you trying to find?
    • An angle? You can use the Triangle Angle Sum Theorem or another angle theorem.
    • A side? See below…
  4. Are you given the lengths of two sides?
    • Yes? You can use the Pythagorean Theorem.
    • No? See below…
  5. Are you given the length of one of the sides?
    • No? You may be able to use similarity, if given the scale factor between two similar triangles. Otherwise, you may not have the tools to determine the length of the missing sides.
    • Yes? See below…
  6. Are you given at least one acute angle measure?
    • No? Can you calculate the missing acute angles using another angle theorem? If not, you may not be able to determine the side lengths.
    • Yes? See below…
  7. Use either given (or determined) acute angle to choose a reference angle.
  8. Using your chosen reference angle, determine if which Trig Ratio will help you find the missing side. The ratio MUST include that missing side.
  9. Set up an equation using your reference angle and trig ratio.
    • sin θ = Opp / Hypot
    • cos θ = Adj / Hypot
    • Tan θ = Opp / Adj
Which tool do I use to solve for the missing side of a right triangle?

Examples

Example # 1

  • Using the given, acute angle as your reference angle, determine which tool would work to solve for variable, the missing side, x.

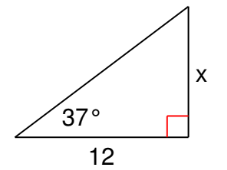
Answer: Tangent.

You have a reference angle (37°) and the adjacent side (12 units).

You need to find the opposite side (x).

So, you need a ratio that includes your given side (adj) and your variable (opp).

That would be Tangent!
Setup: tan 37° = x / 12.

Example # 2